Understanding Rotary Positional Embeddings (RoPE)

Rotary Position Embedding (RoPE) is an advanced technique for encoding positional information within transformer-based language models. Unlike traditional positional embeddings that add or concatenate position vectors, RoPE introduces position by rotating the query and key vectors in multi-dimensional space. This geometric approach enables transformers to capture both absolute and relative positions more effectively, especially for long sequences. In this article, we’ll cover the motivation behind RoPE, its mathematical foundation, key advantages, and practical implementation.

1. Introduction: The Importance of Positional Information

Transformer models have revolutionized NLP, but unlike RNNs and CNNs, they process input sequences as unordered sets. This permutation-invariant property, stemming from the self-attention mechanism, allows for efficient parallelization but makes transformers “blind” to the order of tokens.

The sequential order of words is crucial for natural language understanding. For example:

• “The cat sat on the mat”
• “The mat sat on the cat”

These have the same words but different meanings due to word order. Thus, transformers require a mechanism to encode positional information—this is the role of positional embeddings.

2. Positional Embedding Techniques: Absolute vs. Relative

Absolute Positional Embeddings:
Assign a unique vector to each position in the sequence. The model learns to associate each position with a specific vector, effectively memorizing the absolute position of each token.

Relative Positional Embeddings:
Instead of encoding absolute positions, these focus on the distances between pairs of tokens, allowing the model to leverage relationships based on relative positions.

3. Sinusoidal Positional Encoding

The original transformer model (“Attention is All You Need”) uses sinusoidal positional encoding, which creates unique embeddings for each position using sine and cosine functions:

Where:

• \( pos \) is the position in the sequence,
• \( i \) is the dimension index,
• \( d_{model} \) is the embedding dimension.

Limitations:
Sinusoidal embeddings are absolute and may not generalize well to sequences longer than those seen during training.

4. Rotary Position Embedding (RoPE)

RoPE, introduced by Jianlin Su et al., encodes positional information by rotating embedding vectors in a multi-dimensional space, rather than adding fixed wave patterns. RoPE leverages rotation matrices, providing a geometric and relative way to represent sequential information, which is especially effective for long sequences.

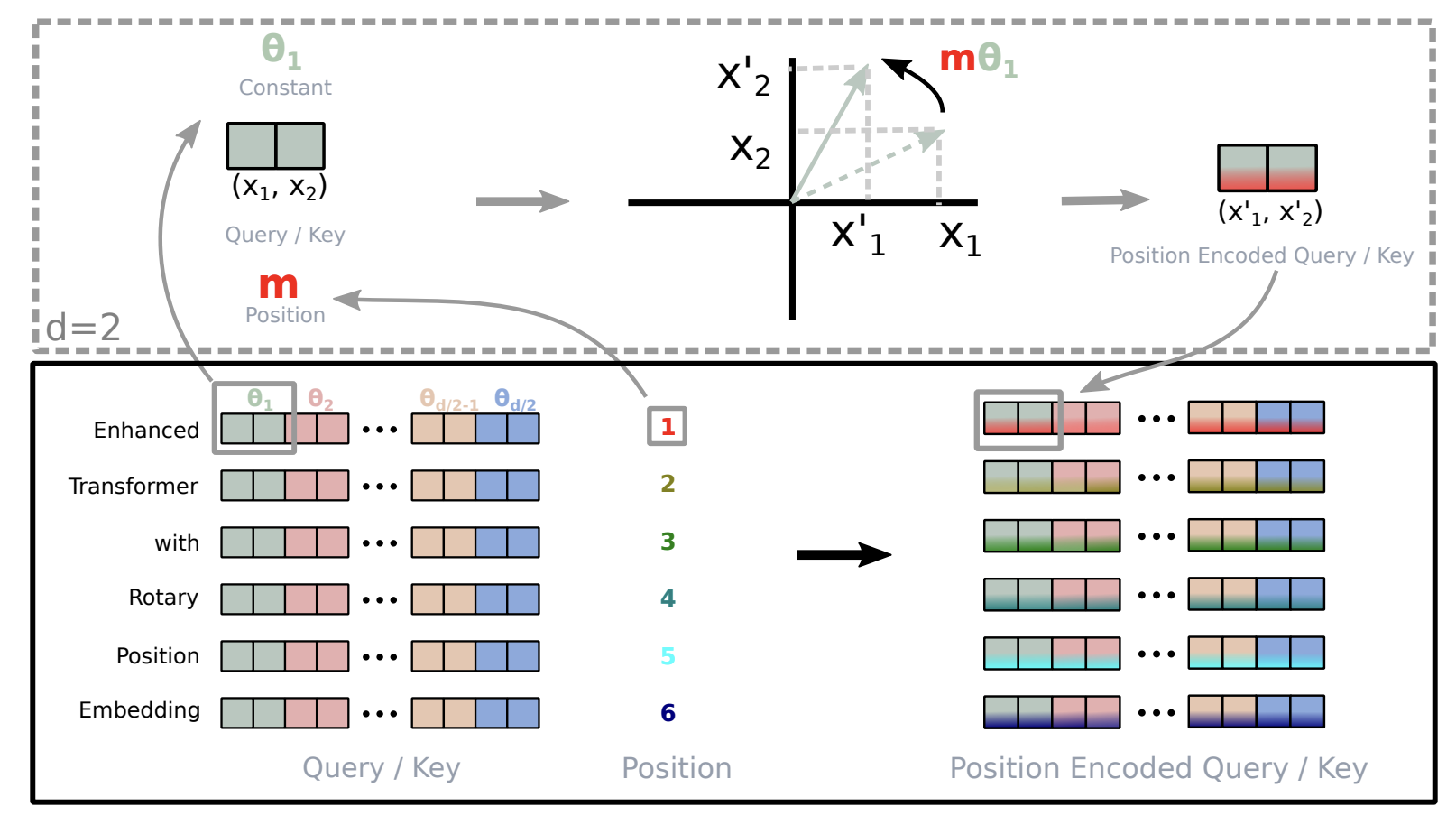Figure: Illustration of Rotary Position Embedding (RoPE).
Image source: RoFormer: Enhanced Transformer with Rotary Position Embedding (Su et al., 2021)

4.1. Mathematical Formulation of RoPE

For a token at position \( pos \) with embedding vector \( x_{pos} \):

where \(\hat{x}_{pos}\) is formed by swapping each pair of even and odd dimensions of \(x_{pos}\), with the odd dimension negated. This operation is applied independently to each pair of dimensions, with each pair using a different frequency.

4.2. RoPE in Two Dimensions

• Initial Embeddings: Tokens A and B have embeddings \( \vec{x}_A \) and \( \vec{x}_B \).
• Positional Rotation: Angles \( \theta_A \) and \( \theta_B \) are calculated for each token.
• Apply Rotation: Each embedding is rotated by its angle using cosine and sine.
• Rotated Embeddings: The new embeddings \( \vec{x}_A' \) and \( \vec{x}_B' \) encode both original and relative positional information.

4.3. Generalizing to Higher Dimensions

For even dimension \( d \), the space is divided into \( d/2 \) subspaces. RoPE combines these using the linearity of the inner product in the self-attention mechanism:

Where:

• \( x_m \) is the embedding at position \( m \),
• \( W_{q,k} \) is the query/key weight matrix,
• \( R_{\Theta, m}^d \) is the rotary matrix.

The rotary matrix is:

Where \( \Theta = \{\theta_i = 10000^{-2(i-1)/d},\ i \in [1, 2, ..., d/2]\} \).

4.4. Incorporating Relative Position Dependency

When RoPE is applied to self-attention, the inner product between query and key becomes:

Where \( R_{\Theta, n-m}^d = (R_{\Theta, m}^d)^T R_{\Theta, n}^d \).

This shows the inner product depends on the relative position \( n-m \) via the rotation matrix.

5. Advantages of RoPE

• Long-Range Context: Effectively captures relationships across long sequences.
• Rotation Invariance: Maintains effectiveness regardless of sequence length.
• Interpretability: Geometric interpretation of positional influence.
• Flexibility: Supports variable sequence lengths and decaying inter-token dependency with distance.

6. Properties of RoPE

6.1. Long-Term Decay

RoPE exhibits a long-term decay property: the inner product between query and key decays as the relative position increases, aligning with the intuition that distant tokens should influence each other less. This is achieved by setting \( \theta_i = 10000^{-2i/d} \).

6.2. RoPE with Linear Attention

RoPE can be integrated with linear attention mechanisms, multiplying the rotation matrix with the outputs of non-negative functions used in linear attention.

7. Theoretical Explanation

7.1. Derivation of RoPE in 2D

By representing query and key as complex numbers, and imposing constraints on their radial and angular components, the functions \( f_q \) and \( f_k \) take the form of rotations:

Where \( e^{im\theta} \) and \( e^{in\theta} \) represent rotations in the complex plane.

7.2. Computational Efficiency

The rotary matrix \( R_{\Theta, m}^d \) is sparse, allowing efficient computation. Instead of direct matrix multiplication, leverage its structure:

Where \( \odot \) denotes element-wise multiplication.

7.3. PyTorch Implementation of RoPE

import torch

def rope_transform(x, base=10000):
    """
    Rotary Positional Embedding (RoPE)
    
    Args:
        x: Tensor of shape [batch, n_heads, seq_len, head_dim]
           (head_dim must be even)
        
    Returns:
        Tensor of same shape as x with RoPE applied
    """
    b, h, s, d = x.shape
    assert d % 2 == 0, "checking for head_dim to be even"
    half_d = d // 2

    # Frequencies (shape: [half_d])
    freq = torch.exp(
        -torch.arange(0, half_d, device=x.device, dtype=x.dtype) *
        (torch.log(torch.tensor(base, device=x.device, dtype=x.dtype)) / half_d)
    )  # [half_d]

    # Positions (shape: [s, 1])
    pos = torch.arange(s, device=x.device, dtype=x.dtype).unsqueeze(1)

    # Angles = outer product [s, half_d]
    angles = pos * freq

    # Precompute cos/sin, shape: [s, half_d]
    cos = torch.cos(angles)
    sin = torch.sin(angles)

    # Broadcast to [1,1,s,half_d] so it matches (b,h,s,half_d)
    cos = cos.unsqueeze(0).unsqueeze(0)  # [1,1,s,half_d]
    sin = sin.unsqueeze(0).unsqueeze(0)  # [1,1,s,half_d]

    # Split x into even/odd channels
    x_even = x[..., 0::2]  # [b,h,s,half_d]
    x_odd  = x[..., 1::2]  # [b,h,s,half_d]

    # Apply rotation
    x_rotated_even = x_even * cos - x_odd * sin
    x_rotated_odd  = x_even * sin + x_odd * cos

    # Recombine into original layout
    x_out = torch.empty_like(x)
    x_out[..., 0::2] = x_rotated_even
    x_out[..., 1::2] = x_rotated_odd

    return x_out


# Example usage
if __name__ == "__main__":
    batch, heads, seq_len, head_dim = 2, 4, 8, 64
    x = torch.randn(batch, heads, seq_len, head_dim)
    x_rope = rope_transform(x)
    print("Input shape:", x.shape)
    print("RoPE shape:", x_rope.shape)

8. Conclusion

Rotary Position Embedding (RoPE) is a novel and effective technique for incorporating positional information into transformer models. By leveraging rotations, RoPE encodes both absolute and relative position information in a geometrically intuitive manner. RoPE offers several advantages over traditional techniques, including better handling of long-range dependencies, rotation invariance, and interpretability. Experimental results show that RoPE enhances transformer performance on a variety of NLP tasks, especially those involving long sequences. RoPE is now being integrated into state-of-the-art models like Mistral, Llama and the latest gpt-oss models.

References

• RoFormer: Enhanced Transformer with Rotary Position Embedding (arXiv:2104.09864)